Research
Explore research from Aaron R. Warren, Associate Professor of Physics at Purdue Northwest University.
Overview
One of the central roles of physics courses is the development of students’ ability to evaluate proposed hypotheses and models. This ability is important not just for students’ understanding of physics, but also to prepare students for future learning beyond physics. In particular, it is often hoped that students will better understand the manner in which physicists leverage the availability of prior knowledge to guide and constrain the construction of new knowledge. My work has focused largely on developing and assessing several techniques that employ hypothetico-deductive (HD) reasoning to aid students in this learning process:
- Employing theoretical evaluation strategies, such as limit-case, special-case, and dimensional analysis, to test a theoretical claim. Examples of theoretical claims to be tested include proposed problem solutions, models of data, and relationships between models.
- Employing statistical evaluation strategies, such as random and systematic error analysis and statistical testing, to assess data-based claims such as the emergence of empirical patterns, consistency of empirical results, and comparisons between model-based predictions and empirical results.
- Employing Bayesian updating to quantitatively revise students’ subjective confidence in both theoretical and empirical claims based on the results of evaluative strategies.
This approach is sufficiently simple for introductory physics students while offering a robust mechanism to guide relatively sophisticated student reflection concerning models, hypotheses, and problem-solutions. Results thus far indicate significant gains in students’ epistemic sophistication that are able to be achieved without an excessive amount of class time. I am currently continuing to study their impact in the context of calculus-based introductory physics.
Selected Presentations
Using Bayesian Updating to Shift Epistemic Beliefs (2018)
Hypothetico-Dedutive Reasoning: Developing Transferable Scientific Abilities (2013)
Quantitative Modeling of Changes in Student Understanding (2011)
Time Series Analysis: Detecting and Measuring Dynamical Changes in Knowledge (2010)
Quantitative Small-N Methodologies (2010)
Selected Papers
Overview
In 1916, Albert Einstein predicted the existence of gravitational wave; ripples in spacetime that would be produced by accelerating masses. Indirect evidence for gravitational waves was first discovered in 1974, but direct detection was only recently achieved by the Advanced LIGO detector on September 14, 2015 when waves produced by the merger of two black holes approximately 1.3 billion light years away were observed. This momentous event marked the beginning of a new era for astrophysics, with many exciting and new results yet to be found.
Using computing clusters owned by Purdue Northwest, my students and I conduct simulations of colliding neutron stars and black holes. The simulations rely on the Einstein Toolkit to numerically solve the difficult partial differential equations that characterize the relativistic behavior of spacetime and the relativistic hydrodynamics of matter in such extreme conditions. We also modify and supplement the Toolkit to enable greater realism in our simulations, for example by utilizing more sophisticated models of neutron star structure than what the ‘vanilla’ Toolkit includes.
My work is currently focused on simulations of binary neutron star (BNS) mergers, addressing several core research questions:
- How can the gravitational waves produced by BNS mergers inform us of neutron star structure, including the nuclear equation of state?
- How are the dynamical mass ejecta produced by BNS mergers dependent upon properties such as mass ratio and magnetization, and how would such properties affect the electromagnetic emissions of the ejecta such as gamma ray bursts and radio flares?
- How well do generalized models of ejecta and gravitational waveforms for BNS mergers fit the results for systems with very high mass ratios over 1.75? How might these models need to be modified for such systems?
Sample Visualizations
Movie 1: A 3D isosurface plot of rest-mass density for a BNS merger with total ADM mass of 2.75 Msol and mass ratio of 1.75 (dx = 0.25M). The Skyrme-Lyon (SLy) equation of state is employed within a 7-segment piecewise-polytrope model. Note the prompt collapse into a black hole after the merger, and the kick given to the black hole, which is traveling at roughly 67 km/s. The physical time scale is shown at bottom left, with the entire movie lasting roughly 25 milliseconds (0.025 seconds).
Movie 2: A 3D isosurface plot of rest-mass density for a BNS merger with total ADM mass of 2.50 Msol and mass-ratio of 2.00 (dx = 0.25M). The Skyrme-Lyon (SLy) equation of state is employed within a 7-segment piecewise-polytrope model. The merger produces a hyper-massive neutron star (HMNS) that will likely collapse to a black hole on a timescale of roughly 100ms.
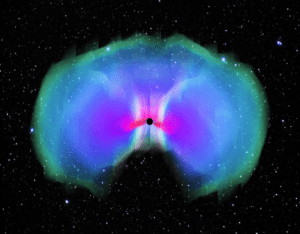Figure 1. A 3D-render of the black hole and surrounding material from a 1.5-1.5 Mo binary, shown 5ms after black hole formation. A quarter of the data has been removed to better show the interior structure of the toroidal distribution surrounding the black hole. Bright pink corresponds to material that is above the neutron drip line (the color coding is different than in Movie 1 shown above).
Movie 3: A color-coded movie of the gravitational wave signal (extracted using the real part of the Weyl scalar, Psi4) generated by the merger of a BH-BH binary. The waves emitted at the beginning are spurious results of the extraction scheme employed.
Selected Presentations
Valparaiso University Astronomy Lecture (2018)
PNC Undergraduate Research Day Keynote Address (2016)
Selected Papers
[Supervised Student Paper] AR Murray, Binary Neutron Star Mergers: Testing Ejecta Models for High Mass-Ratios, Journal of Purdue Undergraduate Research, 10 (2020).
Most of my graduate physics training was in theoretical high-energy physics, under the supervision of Greg Moore. My interest has primarily been on the more mathematical aspects of string theory relating to K-theory and K-homology, and moduli spaces and invariants (such as Donaldson and Seiberg-Witten invariants). Broader topics include algebraic topology, differential topology, differential geometry, noncommutative geometry, conformal field theory, and solitons in both quantum field theory and string theory. I maintain an interest in the field, although my activities are currently focused on physics education and numerical relativity.
Selected Presentations
Modern String Theory (PNC Physics Club Einstein Centenary Colloquium, 2015)
Overview of String Theory (2011)